不同进制有二进制,三进制等。
不同进制有哪些1
1、二进制
二进制作为计算技术中广泛采用的一种数制,两个数字便可表示所有数字,二进制数据是用0和1两个数码来表示的数。它的基数为2,进位规则是“逢二进一”,借位规则是“借一当二”,由18世纪德国数理哲学大师莱布尼兹发现。
当前的计算机系统使用的基本上是二进制系统,数据在计算机中主要是以补码的形式存储的。计算机中的二进制则是一个非常微小的开关,用“开”来表示1,“关”来表示0。
2、三进制
三进制以3为底数的进位制,三进制数有0、1、2三个数码,逢三进一。在计算机发展的早期,采用了一种偏置了的三进制(对称三进制),有-1<一般用T表示>、0、1三个数码,这种三进制逢+/-2进一。

3、四进制
四进制以4为基数的进位制,以 0、1、2 和 3 四个数字表示任何实数。四进制与所有固定基数的计数系统有着很多共同的`属性,比如以标准的形式表示任何实数的能力,以及表示有理数与无理数的特性。
4、四进制
四进制以4为底数的进位制,以 0、1、2 和 3 四个数字表示任何实数。四进制与所有固定底数的记数系统有着很多共同的属性,比如以标准的形式表示任何实数的能力,以及表示有理数与无理数的特性。
5、八进制
Octal,缩写OCT或O,一种以8为基数的计数法,采用0,1,2,3,4,5,6,7八个数字,逢八进1。一些编程语言中常常以数字0开始表明该数字是八进制。八进制的数和二进制数可以按位对应(八进制一位对应二进制三位),因此常应用在计算机语言中。
不同进制有哪些2
一、二进制、八进制、十进制和十六进制是如何定义的?
二进制是Binary,简写为B,二进制只有0和1两个值,计算方法是逢二进一。比如01B+01B(其中B是Binary的首字母,即二进制的简写),结果就是10B,因为逢二进一,低位的1相加后得2就向高位进1;
八进制是Octal,简写为O,八进制是指有0~7这8个值的表示法,计算方法是逢8进1。比如17O+23O=42O,因为逢8进一,低位的7+3=10,10在八进制就是12,加上原来高位的1+2,结果就是42O;
十进制是Decimal,简写为D,十进制即咱们日常使用的0~9。咱们日常做的计算都是十进制的,计算方法是逢十进一,比如21D+11D=32D;
十六进制是Hexadecimal,简写为H,十六进制用数字0-9和字母a-f(或其大写A-F)表示0到15,计算方法是逢16进1,比如1DH+25H=42H,因为逢16进一,低位的D相当于十进制的13,而5可以看成是十进制的5,相加得18,而18-16=2,因此低位的值为2,高位的值即1+2再加上进位1即得4,高位结果就是4,最后结果是42H;
其中计算机采用的是二进制作为基础,在此基础上拓展了八进制、十进制、十六进制等。
二、为什么二进制是基础?
进制如今主要在电技术的数字电路中。如我们经常使的计算机能够识别的语就是进制语。数字电路中的'、低电平;导通、截;开、关;有、无;真、假等等都是二进制表,二进制的逻辑电路使0和1表。
采用二进制主要有以下几个原因:
1、技术实现简单。计算机是由逻辑电路组成,逻辑电路通常只有两种状态,开关的接通和断开,正好用“0”“1”表示。
2、运算规则简单,两个二进制数的和、积运算组合简单。二进制数加法和乘法仅各有3条运算规则( 0+0=0,0+1=1,1+1=1 0和0×0=0,0×1=0,1×1=1 )运算规则简单,有利于简化内部结构,提高运算速度。
3、适合逻辑运算,二进制只有两个数码,和逻辑代数中的“真”“假”相吻合。
4、易于进行转换,二进制数能很容易地转换成八进制、十六进制,也能转换成十进制。
三、为什么有了二进制还需要使用八进制、十进制和十六进制?
八进制和十六进制在现实主要在电技术、计算机编程等领域,这是为了配合二进制使的。上我们说过二进制是计算机所能识别的最直接语,但是二进制的位数太多,不好记录,这时就需要把二进制转化为进制或十六进制。举个例子,买一件商品花费1百块钱,可以使用1元的人民币支付,也可以使用1百元的人民币支付,相对来说,使用百元更方便一点。
十进制主要在常活中,而二进制、八进制、十六进制主要在电技术业。二进制是数字电路、处理器等最直接的语;
八进制以及十六进制都是进存储记忆,但八进制较少使。十六进制来表处理器的寄存器、存储器的地址、数据。
四、进制之间如何转换?
主要思路:二进制数,八进制数、十六进制数可以采用按权展开法转化为十进制数,十进制转化为R进制要分为两部分【这里R进制是泛指,可以代表二进制、八进制、十六进制等】,其中整数部分要除R取余,直到商为0,小数部分要乘R取余直到得到整数。
1. 十进制转R进制
1.1. 十进制转二进制
(1)十进制整数转二进制
十进制整数转换成二进制采用“除2倒取余法”,即将十进制整数除以2,得到一个商和一个余数;再将商除以2,又得到一个商和一个余数;以此类推,直到商等于零为止。
例题: 175D = ___ B
解析:如下图所示,将175除以2,得余数,直到不能整除,然后再将余数从下至上倒取。得到结果:10101111B。
135D = ______ B
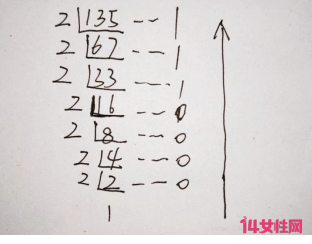
135D = 1000 0111B
(2)十进制小数转二进制
十进制小数转换成二进制小数采用 “乘2取整,顺序排列”法。
具体做法是:用2乘十进制小数,可以得到积,将积的整数部分取出,再用2乘余下的小数 部分,又得到一个积,再将积的整数部分取出,如此进行,直到积中的小数部分为零,或者达到所要求的精度为止。
然后把取出的整数部分按顺序排列起来,先取的整数作为二进制小数的高位有效位,后取的整数作为低位有效位。
例题: 0.68D = ___ B(精确到小数点后5位)
解析:如下图所示,0.68乘以2,取整,然后再将小数乘以2,取整,直到达到题目要求精度。得到结果:0.10101B

1.2. 十进制转八进制
思路和十进制转二进制一样,参考如下例题:
例题: 10.68D = ___ Q(精确到小数点后3位)
解析:如下图所示,整数部分除以8取余数,直到无法整除。小数部分0.68乘以8,取整,然后再将小数乘以8,取整,直到达到题目要求精度。得到结果:12.534Q

1.3. 十进制转十六进制
思路和十进制转二进制一样,参考如下例题:
例题: 25.68D = ______ H(精确到小数点后3位)
解析:如下图所示,整数部分除以16取余数,直到无法整除。小数部分0.68乘以16,取整,然后再将小数乘以16,取整,直到达到题目要求精度。得到结果:19.ae1H
不同进制有哪些3
各种进制相互转换
1、其它进制转换为十进制
方法是:将其它进制按权位展开,然后各项相加,就得到相应的十进制数。
例1: N=(10110.101)B=(?)D
按权展开N=1*24+0*23+1*22+1*21+0*20+1*2-1+0*2-2+1*2-3
=16+4+2+0.5+0.125 =(22.625)D
2、 将十进制转换成其它进制
方法是: 它是分两部分进行的即整数部分和小数部分。
整数部分:(基数除法)
把我们要转换的数除以新的进制的基数,把余数作为新进制的'最低位;
把上一次得的商在除以新的进制基数,把余数作为新进制的次低位;
继续上一步,直到最后的商为零,这时的余数就是新进制的最高位.
小数部分: (基数乘法)
把要转换数的小数部分乘以新进制的基数,把得到的整数部分作为新进制小数部分的最高位
把上一步得的小数部分再乘以新进制的基数,把整数部分作为新进制小数部分的次高位;
继续上一步,直到小数部分变成零为止。或者达到预定的要求也可以。
例2 : N=(68.125)D=(?)O
整数部分小数部分
(68.125)D=(104.1)O

3、二进制与八进制、十六进制的相互转换
二进制转换为八进制、十六进制:它们之间满足23和24的关系,因此把要转换的二进制从低位到高位每3位或4位一组,高位不足时在有效位前面添“0”,然后把每组二进制数转换成八进制或十六进制即可
八进制、十六进制转换为二进制时,把上面的过程逆过来即可。
例3:N=(C1B)H=(?)B
(C1B)H=1100/0001/1011=(110000011011)B
【不同进制有哪些】相关文章:
不同肤质有哪些美白肌肤方法04-08
乙醇和甲醇有什么不同05-24
读不同的书有什么好处06-08
老婆有新欢了有哪些表现05-15
蔬菜有哪些品种04-15
水果之类的有哪些04-16
提神食物有哪些04-20
高端红茶有哪些04-22
冬至的习俗有哪些05-13






