不同进制数之间的转换算法,有二进制转十进制,转八进制,下面介绍不同进制数之间的转换算法.
不同进制数之间的转换算法1
各进制之间是如何进行转换的
一、二进制与其他进制之间的转换:
1:二进制转八进制:
转换方法:利用取三合一法,即从二进制的小数点为分界点,向左(或向右)每三位取成一位。
比如利用这串二进制 1010 0100B = __?__;计算过程如下图所示,得到结果为:244。

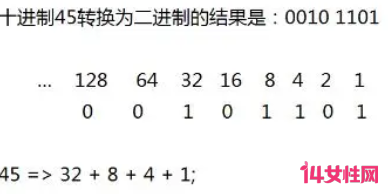
2:二进制转十进制:
转换方法:把二进制数按权展开、相加即得十进制数。(具体用法如下图)
比如利用这串二进制 1001 0110 = __?__;计算过程如下图所示,得到结果为:150。
3:二进制转十六进制:
转换方法:利用取四合一法,即从二进制的小数点为分界点,向左(或向右)每四位取成一位。
比如利用这串二进制1010 0100B = __?__;计算过程如下图所示,得到结果为:a4。
二、八进制进制与其他进制之间的转换:
1、八进制转十进制的方法和二进制转十进制一样。
比如利用这串八进制26Q = __?__;计算过程如下图所示,得到结果为:22。
三、十进制进制与其他进制之间的`转换:
1、十进制转二进制:
转换方法:“除2倒取余”,十进制小数转换成二进制小数采用“乘2取整”。
比如利用这串十进制135D = __?__;计算过程如下图所示,将135除以2,得余数,直到不能整除,然后再将余数从下至上倒取。得到结果:1000 0111。
2、十进制小数转二进制:
十进制小数转换成二进制小数采用 “乘2取整,顺序排列” 法。
转换方法:用2乘十进制小数,可以得到积,将积的整数部分取出,再用2乘余下的小数部分,又得到一个积,再将积的整数部分取出,如此进行,直到积中的小数部分为零,或者达到所要求的精度为止。然后把取出的整数部分按顺序排列起来,先取的整数作为二进制小数的高位有效位,后取的整数作为低位有效位。
比如利用这串十进制0.68D = __?__(精确到小数点后5位);计算过程如下图所示,0.68乘以2,取整,然后再将小数乘以2,取整,直到达到题目要求精度。得到结果:0.10101。
3、十进制转八进制:
转换思路同十进制转二进制一样:
比如利用这串十进制10.68D = __?__(精确到小数点后3位);计算过程如下图所示,整数部分除以8取余数,直到无法整除。小数部分0.68乘以8,取整,然后再将小数乘以8,取整,直到达到题目要求精度。得到结果:12.534。
4、十进制转十六进制:
转换思路同十进制转二进制一样:
比如利用这串十进制25.68D = __?__(精确到小数点后3位);计算过程如下图所示,整数部分除以16取余数,直到无法整除。小数部分0.68乘以16,取整,然后再将小数乘以16,取整,直到达到题目要求精度。得到结果:19.ae1。
四、十六进制进制与其他进制之间的转换:
1、十六进制转十进制:
比如利用这串十进制23daH = __?__D;计算过程如下图所示,得到结果:9178D。
不同进制数之间的转换算法2
二进制与十进制之间的转换是怎么样的
十进制转二进制分为整数转二进制和小数转二进制。
1、采用"除2取余,逆序排列"法(整数转二进制):首先用2整除一个十进制整数,得到一个商和余数。然后再用2去除得到的商,又会得到一个商和余数。重复操作,一直到商为小于1时为止。然后将得到的所有余数全部排列起来,再将它反过来(逆序排列)。

2、采用"乘2取整,顺序排列"法(小数转二进制):用2乘十进制小数,可以得到积,将积的整数部分取出。再用2乘余下的小数部分,又得到一个积,再将积的整数部分取出。重复操作,直到积中的.小数部分为零,此时0或1为二进制的最后一位,或者达到所要求的精度为止。如果小数的整数部分有大于0的整数时,将整数部分和小数部分先单独转为二进制,再合在一起就可以了。
二进制转换为十进制时要从右到左用二进制的每个数去乘以2的相应次方,小数点后则是从左往右。如果首位是0就表示正整数,如果首位是1则表示负整数,正整数可以直接换算,负整数则需要先取反再换算。因为计算机内部表示数的字节单位是定长的。如8位、16位、32位。所以位数不够时,高位补零。
不同进制数之间的转换算法3
几进制与二进制之间存在特殊关系
10进制255和2进制存在特殊关系。
1、IP地址是一个32位的二进制数,通常被分割为4个“8位二进制数”(也就是4个字节)。
2、IP地址通常用“点分十进制”表示成(a.b.c.d)的形式,其中,a,b,c,d都是0~255之间的十进制整数。例:点分十进IP地址(100.4.5.6),实际上是4个8位的位二进制数(01100100.00000100.00000101.00000110)。一共32位
3、为什么是255为上限呢?因为IP地址的每一个10进制数占8位二进制,最大的是11111111,也就是255。
十六进制以什么加以标识
十六进制中用A,B,C,D,E,F(字母不区分大小写)这六个字母来分别表示10,11,12,13,14,15加以标识。
十六进制(简写为hex或下标16)是一种基数为16的计数系统,是一种逢16进1的'进位制。
16进制多位数字母需要换算,换算方法如下:
16进制数的第0位的权值为16的0次方,第1位的权值为16的1次方,第2位的权值为16的2次方……
所以,在第N(N从0开始)位上,如果是是数 X (X 大于等于0,并且X小于等于 15,即:F)表示的大小为 X*16的N次方。
如今的16进制则普遍应用在计算机领域,这是因为将4个位元(Bit)化成单独的16进制数字不太困难。1字节可以表示成2个连续的16进制数字。可是,这种混合表示法容易令人混淆,因此需要一些字首、字尾或下标来显示。
16进制转二进制的方法介绍如下:
在二进制的表示方法中,每四位所表示的数的最大值对应16进制的15,即16进制每一位上最大值,所以,我们可以得出简便的转换方法,将16进制上每一位分别对应二进制上四位进行转换,即得所求:
例:2AF5换算成2进制
第0位: (5)16 = (0101) 2
第1位: (F)16 = (1111) 2
第2位: (A) 16 = (1010) 2
第3位: (2) 16 = (0010) 2
得:(2AF5)16=(0010.1010.1111.0101)2
【不同进制数之间的转换算法】相关文章:
不同进制转换对照表06-29
不同进制数怎么理解06-29
不同进制数对照表如何记忆06-29
不同进制的换算06-29
不同进制数对照表要背吗06-29
不同进制数的对照表15-2306-29
不同进制有哪些06-28
二进制对应16进制表06-29
如何转换职场轨道04-19