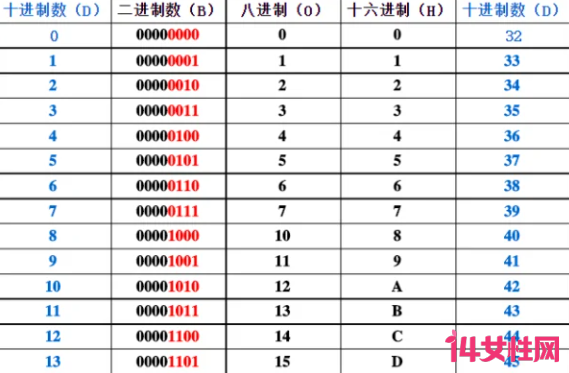
进制的对应表,不同进制之间的转换比较复杂,需要牢记进制的转换方法,必要时候记住进制的对应表。
进制的对应表1
1.基本概念
数位:指数字符号在一个数中所处的位置。
基数:指在某种进位计数制中数位上所能使用的数字符号的个数。例如十进制的基数为10
2 计算机语言中常用的进制及表示方法
在计算机汇编语言中,常用的进制有二进制、八进制和十进制。
数制的表示有2种方法,一种表示方法是数字下标法,对于不同进制的数可以将它们加上括号再用数字下标表示进制:
例如:(110010011111)2 代表二进制数 ; (6137)8 代表八进制数
另一种是用后缀字母表示进制:
二进制 B (binary)
八进制 O (octal)
十进制 D (decimal)
十六进制 H (hexadecimal)
3 常见进制的运算规则
(1)二进制:逢二进一
基数为2,数值部分用两个不同的数字0、1来表示。
如:二进制数1101.01转化成十进制例如:二进制数100011转成十进制数可以看作这样:
数字中共有三个1 即第六位一个,第二位一个,第一位一个(从右到左),然后对应十进制数即2的'0次方+2的1次方+2的5次方, 即
100011=32+0+0+0+2+1=35
(2)十进制:逢十进一
基数为10,数值部分用0、1、2、3、4、5、6、7、8、9来表示.
(3)十进制整数转二进制距离说明:
如:255=(11111111)B
255/2=127=====余1
127/2=63======余1
63/2=31=======余1
31/2=15=======余1
15/2=7========余1
7/2=3=========余1
3/2=1=========余1
1/2=0=========余1
789=1100010101(B)
789/2=394 余1 第10位
394/2=197 余0 第9位
197/2=98 余1 第8位
98/2=49 余0 第7位
49/2=24 余1 第6位
24/2=12 余0 第5位
12/2=6 余0 第4位
6/2=3 余0 第3位
3/2=1 余1 第2位
1/2=0 余1 第1位
1101.01(2)=1*20+0*21+1*22+1*23+0*2-1+1*2-2=1+0+4+8+0+0.25=13.25(10)
进制的对应表2
十进制转成二进制
正整数转成二进制。要点一定一定要记住:除二取余,然后倒序排列,高位补零。
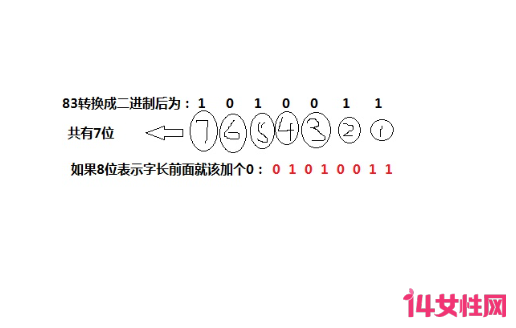
也就是说,将正的十进制数除以二,得到的商再除以二,依次类推知道商为零或一时为止,然后在旁边标出各步的余数,最后倒着写出来,高位补零就OK咧。还是举例说明吧,比如83转换为二进制,如图下所示操作。

83除以2得到的'余数分别为1100101,然后咱们倒着排一下,83所对应二进制就是1010011
计算机内部表示数的字节单位是定长的,如8位,16位,或32位。所以,位数不够时,高位补零,所说,如图所示,83转换成二进制以后就是。01010011,也即规范的写法为(83)10=(01010011)2.赶紧记住吧。
方法:先是将对应的正整数转换成二进制后,对二进制取反,然后对结果再加一。还以83为例,负整数就是-83,如图所示为方法解释。最后即为:(-83)10=(10101101)2.

小数转换为二进制的方法:
对小数点以后的数乘以2,有一个结果吧,取结果的整数部分(不是1就是0喽),然后再用小数部分再乘以2,再取结果的整数部分……以此类推,直到小数部分为0或者位数已经够了就OK了。然后把取的整数部分按先后次序排列就OK了,就构成了二进制小数部分的序列,举个例子吧,比如0.125,如图所示。

进制的对应表3
十进制转成十六进制
1、将二进制数从右到左每四位分组。例如,对于二进制数10111010,我们可以将它分成 1011 1010 三个组。
2、将每组二进制数转换为十六进制数。对于每个四位二进制数,我们可以使用以下表格将其转换为相应的十六进制数:
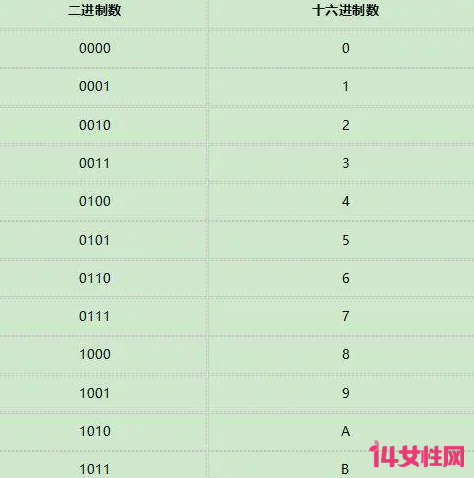
例如,对于二进制数1011,它转换为十六进制数为B。
将每组的十六进制数按照原来的.顺序排列。例如,对于二进制数10111010,它转换为十六进制数为BA。
为了更好地理解这个过程,我们可以看一个例子。将二进制数1101101010101011转换为十六进制数,我们可以把它分成4位一组得到1101 1010 1010 1011,然后将每组转换为十六进制数得到D A A B,最后按照原来的顺序排列得到0xDAAB。
通过上述的操作就可以将二进制数转换为十六进制了。如果你觉得这样转换太麻烦的话,我们还可以使用一些计算工具来辅助转换。比如说可以使用计算器软件来进行进制转换的操作。
【进制的对应表】相关文章:
二进制对应16进制表06-29
时辰表对应时间06-27
生肖对应时辰表06-28
十二时辰表对应的生肖06-26
十二时辰表对应的时辰06-26
十二时辰表对应的时辰图06-26
二进制和16进制06-29
十二时辰表对应的时辰是什么06-26
十二时辰表对应的时辰和时辰06-27






